地貌的演化由构造、岩性和气候等因素共同控制,这一认识为通过地表地貌重建过去的地质过程提供了依据。河流地貌是地表广泛分布的地貌类型,其形态、结构和演化受上述因素控制,因而其中包含着重要的构造运动时空演化的信息。前人曾成功利用河道的形态提取构造抬升的空间分布(Kirby and Whipple, 2012)以及时间演化(Pritchard et al., 2009)等信息。然而由于其影响因素众多、控制机制较为复杂,所以相关的理论和技术仍在进一步发展中。
在河流地貌的研究中,近年来产生了χ变换的分析手段(Perron and Royden, 2012),并在很多重要的研究中得以应用。如Goren等(2014)使用河道纵剖面反演区域的构造抬升历史、Willett等(2014)使用χ值对比判断分水岭的迁移方向等,都以χ变换作为理论基础。研究在理想的条件下可以得到较为可靠的结果,例如当区域的构造、岩性和气候等条件不变的情况下,分水岭两侧χ值的差异能指示分水岭的迁移方向(Willett et al., 2014)。然而当这些条件在时空上分布不均匀时,χ值可能会失去对分水岭迁移的指示作用(Whipple et al., 2017; Forte et al., 2018)。此外在河道纵剖面反演抬升历史的研究中,也需要剔除构造、岩性和降水等因素空间差异的影响,以获得较为可靠的构造抬升历史(Goren et al., 2014)。然而自然界中较为普遍的情况是,构造、岩性和气候等条件在空间上往往是分布不均匀的。如果不了解这些因素对χ值的影响,将会限制其进一步的拓展与应用。
地震动力学国家重点实验室博士生周朝,在谭锡斌研究员指导下,基于前期的研究成果(Zhou et al., 2022),通过公式推演量化了差异抬升、岩性或降水、侵蚀基准面的差异等因素对分水岭两侧χ值差异的影响(图1)。在此基础上使用数值模拟对公式的可靠性进行了验证(图2),并给出了两个自然实例的典型应用(图3-4)。在内蒙古乌拉山的例子中,根据公式估算得到其南北两侧山前活动断层的垂向滑动速率比值约为0.2(图3)。在山西系舟山的例子中,根据公式判断该地区主分水岭呈现向南迁移的趋势(图4)。
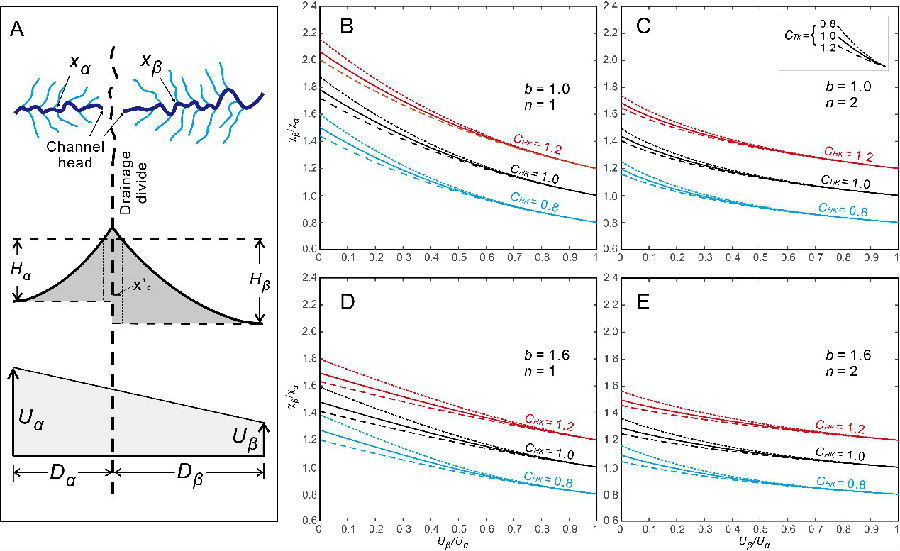
图1 根据公式绘制的抬升速率比值和χ比值的关系图

图2 使用数值模拟验证抬升速率比值对χ比值的影响
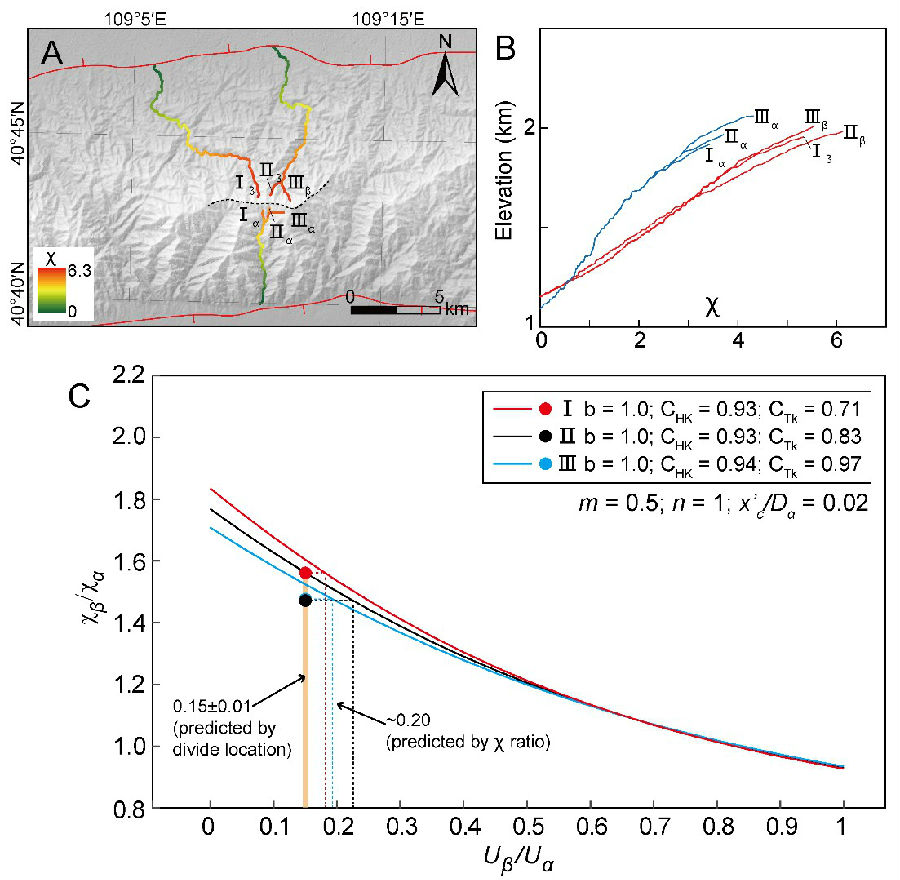
图3 内蒙古乌拉山χ比值结果及推测的山前断层活动速率比值
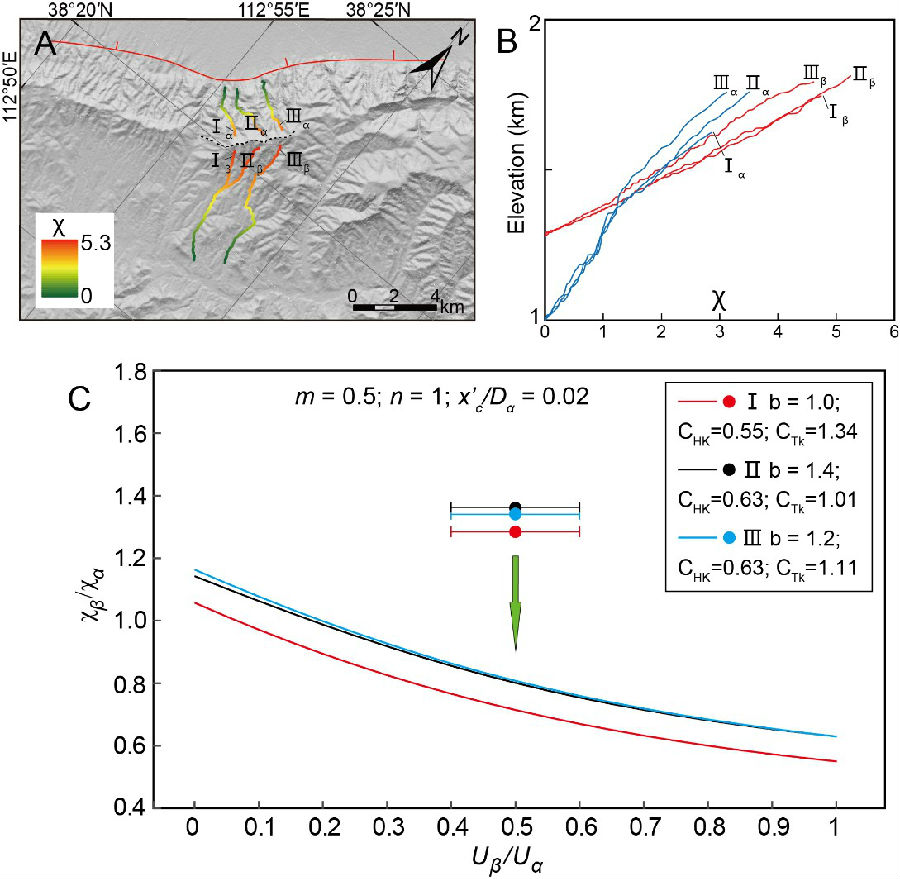
图4 山西系舟山χ比值结果及推测的主分水岭迁移方向
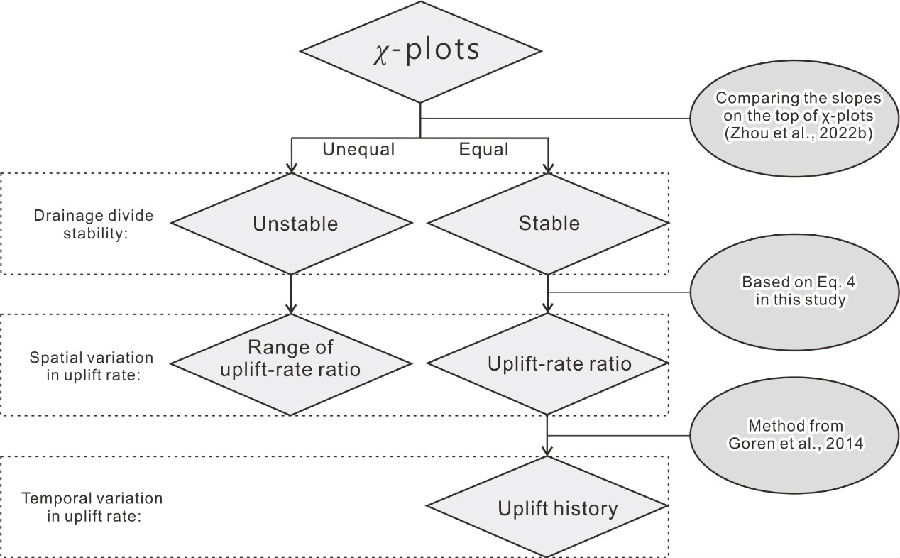
图5 本研究建议的通过χ-高程图提取构造信息(包含抬升速率的空间和时间差异)流程图
本研究得到的新公式不仅可以有助于通过地形地貌进行构造信息提取(图5),而且可以将χ值对比法(用来判断分水岭稳定性)拓展到地质条件较为复杂的地区。虽然此方法仍存在一定误差,但对进一步理解构造、岩性和气候等因素与河流地貌的相互作用关系起到了推动作用。本研究得到了中科院百人计划项目(E2K2010010)和地震动力学国家重点实验室基本科研业务专项(LED2021A02)的资助。相关文章于2023年2月20日在线发表于国际地貌学主流杂志《Geomorphology》:
Chao Zhou, Xibin Tan*, 2023. Quantifying the influence of asymmetric uplift, base level elevation, and erodibility on cross-divide χ difference. Geomorphology, https://doi.org/10.1016/j.geomorph.2023.108634
主要参考文献:
Kirby, E., Whipple, K.X., 2012. Expression of active tectonics in erosional landscapes. J Struct Geol 44, 54-75. https://doi.org/10.1016/j.jsg.2012.07.009.
Pritchard, D., Roberts, G.G., White, N.J., Richardson, C.N., 2009. Uplift histories from river profiles. Geophys Res Lett 36. https://doi.org/10.1029/2009gl040928.
Perron, J.T., Royden, L., 2012. An integral approach to bedrock river profile analysis. Earth Surface Processes and Landforms 38, 570-576. https://doi.org/10.1002/esp.3302.
Goren, L., Fox, M., Willett, S.D., 2014. Tectonics from fluvial topography using formal linear inversion: Theory and applications to the Inyo Mountains, California. Journal of Geophysical Research: Earth Surface 119, 1651-1681. https://doi.org/10.1002/2014jf003079.
Willett, S.D., McCoy, S.W., Perron, J.T., Goren, L., Chen, C.Y., 2014. Dynamic reorganization of river basins. Science 343, 1117. https://doi.org/10.1126/science.1248765.
Whipple, K.X., Forte, A.M., DiBiase, R.A., Gasparini, N.M., Ouimet, W.B., 2017. Timescales of landscape response to divide migration and drainage capture: Implications for the role of divide mobility in landscape evolution. Journal of Geophysical Research: Earth Surface 122, 248-273. https://doi.org/10.1002/2016JF003973.
Forte, A.M., Whipple, K.X., 2018. Criteria and tools for determining drainage divide stability. Earth Planet Sc Lett 493, 102–117. https://doi.org/10.1016/j.epsl.2018.04.026.
Zhou, C., Tan, X., Liu, Y., Shi, F., 2022a. A cross-divide contrast index (C) for assessing controls on the main drainage divide stability of a mountain belt. Geomorphology 398, 108071. https://doi.org/10.1016/j.geomorph.2021.108071.



