钾-氩(K-Ar)和氩-氩(40Ar-39Ar)测年实验室始建于1979年。仪器为英国VG公司生产的MM-1200静态质谱仪和与之相联接的全金属样品熔样系统及稀有气体纯化系统。2005年引进GV公司生产的MM-5400(He型)质谱仪。利用Ar-Ar法和K-Ar同位素稀释法可开展地质体经历的构造热过程研究和火山岩的精确测年研究,特别是活动火山的测年研究。
2008年汶川地震的发生后,社会对实验室提出新的要求,“进行地震相关的基础研究”。实验室开始转型,开始了21Ne宇宙成因核素测年方法的研究,建立的21Ne测年实验流程。
主要成员:马严、武颖、李大明 (联系电话:010-6200 9190)
K-Ar(40Ar/39Ar)发展历史
早在上世纪五十年代,科学家们就建立了利用K的放射性衰变进行K-Ar同位素年龄测定的理论基础,其基本原理是根据放射性元素的衰变规律,通过测试矿物中母体K和子体Ar的量来计算年龄。然而一方面,由于样品的K含量和Ar的含量必须分开测量,使得测量的精度低;另一方面由于过剩氩和氩丢失现象的发现,有时会得到没有地质意义的年龄。60年代中叶40Ar/39Ar定年技术是在K-Ar发的基础上发展起来的,这种方法不仅可以克服常用的K-Ar法年龄测定的某些局限性,还具有独特的优点,使得该法被广泛应用于测定各种矿物岩石的年龄,探索区域性乃至全球性的重要地质问题。上个世纪80年代末,随着钾长石MDD假说的提出,Ar-Ar法在构造地质学方面的研究掀开了新的一页。
40Ar/39Ar定年的基本原理
由放射性衰变定律可以得到同位素地质年代学的基本方程:

式中P为放射性母体原子数,D为放射成因子体原子数,λ为母体的衰变常数。
40K具有双重放射性衰变(40K→40Ar和40K→40Ca),K-Ar法计时只关心40K→40Ar 衰变分支,上述年龄计算基本方程需要作适当修改。分数fAr 是40K→40Ar 分支有关部分衰变常数(λe +λ′e)与40K(总)衰变常数(λ)之比:

代入方程(1)得:

式中40Ar*/40K是现在样品中放射成因40Ar*与母体40K的比值。衰变常数是已知的,测定样品中的40Ar*和40K 的量即可计算出样品的年龄。
对于40Ar/39Ar法,由39K经快中子活化产生的39Ar与样品中的40K成正比,因为自然界40K/39K比值基本上是一个常数。因此,40Ar*/39ArK 比值与年龄值成正比。但用39ArK 直接代替方程(3)的40K显然不合适,因为中子活化所产生的39ArK明显取决于中子辐照时间、中子通量以及能量高于发生原子核反应临界能量的中子比率等因素,所以需要采用不同的处理方法。方程(3)可以改写成:

根据(Mitchell, 1968)的推导,样品中子活化过程中由39K产生的39ArK可以用下式表达:
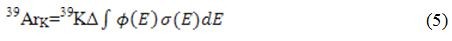
式中39K是中子活化前样品中的39K原子数,39ArK 是样品中39K产生的39Ar原子数,Δ为中子活化时间,Φ(E)是能量为E的中子能量,σ(E)是产生39K(n,p)39Ar反应能量为E的中子俘获横截面积。
正如Grasty et al. (1966)和Mitchell(1968)所指出,定义一个中子活化参数J
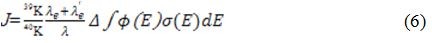
式(2-4)除以式(2-5),并把式(2-6)代入得

由方程(2-7)整理得40Ar–39Ar法年龄计算公式

显然只要辐照参数J能够确定,只需测定从活化样品中提取出来的气体的40Ar*/39ArK 比值,就可以根据方程(8)计算出样品的年龄。40Ar/39Ar年龄计算公式(8)是K–Ar法年龄计算公式(3)的修正形式。
由方程(5)和(6)可知,与39K中子活化产物39ArK相关的辐照参数J取决于照射时间、中子通量、中子俘获横截面积。由于难以准确测定样品所接受的快中子积分剂量,Merrihue et al.(1966)建议采用一个已知年龄的样品(标准样品)与待定年样品一起进行中子活化,以监测这一剂量。方程(7)整理得

已知标准样品的年龄trs(可用传统K–Ar法测得),由方程(9)可知,只要测定标准样品的(40Ar*/39ArK)rs比值,辐照参数J即可确定。然后把J值和待定年样品(与标准样品一起辐照)的40Ar*/39ArK比值代入方程(8),即可计出样品的年龄。
把方程(9)代入方程(8)得:

式中下标s表示待定年样品。
由方程(8)和(10)可知,只要知道样品的同位素比值,即可计算出样品年龄。
K-Ar(40Ar/39Ar)主要测年对象
火成岩全岩、角闪石、云母、长石等单矿物以及粘土矿物中伊利石的测年实验研究。样品量,一般小于100毫克。
主要仪器:MM1200惰性气体质谱仪

21Ne测年的基本原理
(1) 暴露测年原理
地表暴露测年是依据深埋于地表以下的岩石,由于宇宙射线受到屏蔽,宇宙成因核素积累量几乎为零,当岩石暴露或接近于地表后,受宇宙射线粒子轰击而产生宇宙成因核素并在样品中积累。地表样品中核素含量取决于地表物质暴露在宇宙射线中的时间。因此,已知地表样品中宇宙成因核素的生成速率和核素含量,即可测定样品暴露于地表的年代。
样品暴露地表的过程中,宇宙成因核素的积累量N(t, z)与样品的暴露时间t及地表侵蚀速率ε具有以下关系:
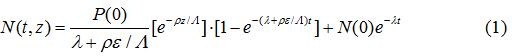
其中,N(t,z)是t时刻岩石中深度为z处的核素原子个数(atom·g-1);P(0)为核素在岩石表面的生成速率(atoms·g-1·a-1);ρ为岩石密度(g·cm-3);Λ为宇宙射线粒子的吸收自由程(attenuation coefficient) (g·cm-2);ε为地表剥蚀速率(cm·a-1);N(0)为样品初始暴露地表时原地生成宇宙成因核素含量(atom·g-1);λ为宇宙成因核素的衰变常数(a-1)。
若假设:①样品中继承性组分含量可以忽略不计;②系统保持相对封闭,即除侵蚀外无核素流失,以及除原地生成外无其他输入方式;③生成速率已知并随时间保持恒定;④核素浓度全部集中于地表,即消除对深度的依赖关系,则上式可简化为:

对于稳定核素21Ne而言,衰变常数λ趋于0;若忽略地表剥蚀,即ε=0,只要测量出地表岩石样品中宇宙成因核素浓度N(t,0),即可通过下式这一简单关系,得到样品的最小暴露年龄tmin:

若考虑地表侵蚀作用的影响,在稳态侵蚀下,稳定核素在岩石中的积累也可达到动态平衡状态。侵蚀作用越强烈,核素达到动态平衡浓度的时间越短(见图2所示),测年上限也相应越低。
(2) 埋藏测年原理
沉积物埋藏测年是基于同一岩石或矿物中,具有不同半衰期的一对宇宙成因核素的浓度比值会随埋藏时间发生变化而进行定年。地表岩石在暴露于地表的过程中,宇宙成因核素生成并在样品中积累。当这些地表岩石经搬运、沉积等过程被埋藏后,宇宙成因核素停止生成,仅进行放射性衰变。核素对的生成速率比值是固定的,不受纬度和海拔的影响。由于不同核素的衰变速率不同,造成核素对浓度的比值随埋藏时间的增加而发生变化,因此,通过测定沉积物中一对半衰期不同的宇宙成因核素的含量及比值,即可计算出沉积物样品的埋藏年龄。沉积物满足①相对于岩石样品在地表暴露的时间和埋藏时间而言,埋藏过程发生较快,时间较为短暂,可忽略不计;②埋藏深度足以阻断宇宙射线的辐射,是使用宇宙成因核素埋藏测年方法对沉积物定年的前提。
埋藏测年注重研究的是地表岩石样品在接受辐射后迅速埋藏,宇宙成因核素停止生成后进行放射性衰变的时间。因此,埋藏年龄的确定同时涉及到沉积物埋藏前后的历史。以21Ne- 10Be核素对为例,首先,假定地表样品在暴露时间T内生成的21Ne和10Be含量分别为NNe(0) 和NBe(0),样品被快速埋藏,并且埋藏后不再受宇宙射线辐射影响,则经历了时间t的埋藏历史后,21Ne和10Be的含量NNe(t) 和NBe(t)可分别表示为:
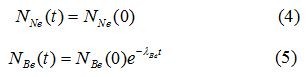
若样品在地表的暴露时间T远小于10Be的半衰期,则:
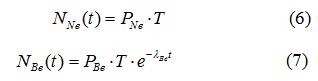
联合(6)、(7)两式,可得到埋藏时间t和埋藏前的暴露时间T。若样品在埋藏前经历了较长的暴露历史,暴露时间T>>1/(λ+rε/Λ),核素含量已达到动态平衡,且地表处于稳态侵蚀状态,则核素的浓度可分别表示为:
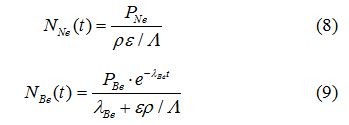
联合(8)、(9)两式,可得到埋藏时间t和埋藏前地表侵蚀速率ε。
21Ne法主要测年对象:
石英、橄榄石、辉石、角闪石、黑云母;最常用矿物是石英
主要仪器:GV5400惰性气体质谱仪

近期发表文章:
1. 马严, 武颖, 庞建章, 张会平, 俞晶星, 郑德文. 宇宙成因21Ne暴露测年方法的初步建立及检验. 科学通报, 2014, 59 (27): 2707-2713
2. 杨静, 郑德文, 邱华宁, 武颖, 王伟涛, 许英霞. 吐哈地区表生黄钾铁矾40Ar/39Ar定年及其对晚中新世风化前锋拓展速率的限定. 科学通报, 2014, 59 (30): 2956-2963
3.Ma, Y., Wu, Y., Li, D.M., Zheng, D.W., 2015. Analytical procedure of neon measurements on GV 5400 noble gasmass spectrometer and its evaluation by quartz standard CREU-1. International Journal of Mass Spectrometry. 380, 26-33.
4. Yang Jing, Zheng Dewen, Li Daming et al. The Preliminary Investigation of Diffusion Kinetics of Supergene Yavapaiite and Its Significance. Scince in China, (D), 2012
5. 马严,武颖,庞建章,张会平,郑德文.宇宙成因核素21Ne测年原理和应用. 地震地质,2015, 31(1):doi:10.3936/j.issn.0253-4697.2015.0
6.Yang Jing, Zheng DeWen, Chen Wen, Qiu HuaNing, Wang Weitao, Wu Ying, Xu Yingxia. 40Ar/39Ar geochronology of supergene K-bearing sulfate minerals: Cenozoic continental weathering and its paleoclimatic significance of Tu-Ha Basin, nortern Tibetan plateau. P.P.P. (in press)



